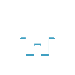象棋弈修大象无形第八十八章一车破双士随想之把简单的事情复杂化。

我经常看象棋初阶杀法，有时候看到特别精彩的残局走法，觉得不可思议，甚是奇妙！当一看书面挂着初阶二字，特别不能理解。这么好的走法，奇思妙想怎么只是初阶走法，那么大师，大大师级别又会怎样？又是怎样的？不知道你有没有这种疑惑。

就好像学习小学，初中，高中，大学，硕士博士一样，你觉得好的时候，别人一看说你才小学水平？是不是很受打击？后来偶尔想到象棋与学习小学初中高中的学习是有区别的，就像数学，小学识数，初中代数，高中微积分不同阶段基础不同，所有知识点不同。而象棋不一样，象棋不论初学者还是大师，最后的杀法总会归结到最后对车马炮兵卒士相的运用上，基础杀法虽然是最基础的入门的，但也是最高深的，你达到很高很高的高度最后还是用这几种杀法杀敌。所以这里简单说的是初阶即高阶，就像武术你如果能够在基础杀法基础上开出新的领域，那么你也是一代宗师！

话说这么多，闲聊之言，言归正传，我们还是学习更简单的吧。看图说话，一车对抗双士。前面说过一车不能够战胜士相全，不是因为价值子力没有士相之和大。我们从牵制，攻防，无损得子角度进行了简单描述。看这里，双士，如果拿掉将帅，用车斗双士，如果双士始终连着，那么一车永远不能消灭一士。原因何在？有根，一个子守护着另一个子，受到攻击时候，对方也会受到后援的攻击。

就是说如果双士连在一起，不动，一车不能破防，不能无损得子。两个子力不动，这是没有其它任务情形下，而一般情形下是相反的。如图在一车对双士将军的时候

（88.1）

黑方考虑如何不丢士的时候，红方考虑如何能赢棋。这两个考虑不是一个问题，关键是保存双士与输不输棋没有绝对关系。黑方知道丢士后必然输棋，现在去想的是能否不丢士，不丢士能否保持抗衡。

一车的确不能杀双士，那是因为象棋中没有游戏里不破防的说法。象棋中每个子力能够攻击别人同时也能够被别人攻击，而且都是攻击一次，没有说攻击一次不死的说法。简单话说就是都有攻击力，而防御力为零，受到攻击就会死亡。而生根后援的方式只是保证对方吃掉己方子力后对方会付出代价。不是说真正能够阻止攻击。对方没有攻击的原因是价值不对等，考虑对方子力价值可能大于己方子力价值。当然以后除了子力价值还有考虑配合价值即势的一种。

如图红方如果平车将军黑方，只好回到中路，这样红方没有吃掉士，如果红方平车一侧，黑方则再次歪将。好像红方不能拿对方怎么样。可是，黑将回到中路后，黑将红帅一条线，红方牵制黑方双士黑将都不能移动了。黑方造成困死局面。棋盘中每一个子力在具有一步中都可以不走，但具体那一步时候却不能所有子力都不走，需要走动至少一个子力，这样就形成黑方没有子力可走的局面。这里红方虽然单子不破连，但将军死棋不是必须消灭所有子力，不等于必须杀光所有子力。再有此时如果改黑方走，黑将进一，红车平将军，黑方支士，红帅平肋助攻，黑士相连，形成图2局面。

（88.2）

此时红方车四平三，黑方士5进4；车三进四捉士，黑方退士连防；进车将军，黑将退1；黑将退，士露出被杀。这样红方得士。

我们都知道红方必然能够胜利，或者困毙或者破士胜。那么你怎么证明红方一定能够破士而胜？

你说车帅胜车双士是因为黑士要保护黑将，红方帅能够牵制一个士吗？我觉得也不全然是这样。上面明面上是由于一个士被牵制，另一个士失去保护被攻击。但是你是如何证明红车一定能够捉到士呢？根据上面例子你可能会说红方帅能够起到牵制作用，最后一定破士。上面只是所有形式中的一种，不能表示所有形。

上面论证车对双士时候利用等招，由于双士有一个士不能动，车必然能够破掉。那么此时增加黑将防守，红车还有能力破掉一士吗？

（88.3）

我们再回到双士一车对抗局面，没有将帅，此时双士连虽然红车不能杀掉士。但是由于必须走棋这种规则，火力覆盖一士的时候，利用停顿杀对方。双士连必然有一个士不能动，牵制对方不能动的那个士，移动一步后不改变继续攻击整体，那么对方另一个士的活动造成，双士不能继续联防，所以丢子。

再看双士对车帅，这样红方车不动，利用帅走闲棋牵制最后得子。在双士对帅车中，双士被迫，是因为等招。一个车能够牵制不动的那个士，另一士必然被迫走动，造成双士脱离联系，被无损捉子。

在复杂一些，黑方加一将形成双士将，红方车帅，此时又要加入黑将对士的守护，是否增加红方破掉双士的难度？黑将的存在同时又是被攻击的目标，新的增加红车对黑将的攻击因素。提出红方是先能够破士还是先破将呢？红方是先一步攻破单一的将呢？还是破掉双联的士呢？当然这种想法是假设将与其它子力是平等的。

当然黑将与士是不等的，这种假想有些费脑袋。这里我们不在纠结将军问题，而是思考另一问题，此时红方能否无损得士？你还别说，一个车还真拦不住双士黑将的防守。车看住双士的时候，黑将能够自由活动。一个车不能同时看住双士和黑将。看住双士，黑将活动；看住黑将，黑士活动。一车难以破掉双士将三个子力的活动。

再把双士换成单士一将，由于黑士将在九宫活动，竖向看只有三条道路，车追逐黑将时候，黑将能够两条道路来回选择，看似不能拿黑方怎么样，实则红车驱逐黑将一路后，在驱逐黑士（设原来在肋道）回中，此时黑将在中路那么黑将中士一线；如果黑将在肋道，那么在去车追逐则黑将回中，这样必然造成黑将黑士一线，这样就会形成车牵制将士然后利用等招造成黑方丢子。这样我们就论证了不论是两个士还是一个士一个将两个子力，由于活动范围有限，必然造成车牵制两个子力，造成无损取子条件。这样由于活动范围一定造成车能够抗衡两个子力相互防守，红方车必然胜利。而三个子力双士将对车的时候，一车已经难以抗衡，不能无损破防。这样看象棋中即使在有限范围内一个子力最多对抗两个子力，能够无损得子。面对三个子力时候，也不能破防。

这样一个子力最多对抗“两个子力能够无损得子，多余两个时候已经无能威力”的经验性结论。———弈修随想记。

当我们把这个结论运用到通常说的一车对双士的时候即一车一帅对双士一将，红帅牵制黑将. 这样又变成一车对双士，红方能够胜利。当然这是一种外推。至于能否成立还在两可两不可之间。

这里对不对先拿着结论来用，象棋中一个子力最多能够破防两个子力，两个子力能够破防三个子力，三个子力能够无损破防四个子力等等等。———哈哈，对不对拿着先用。不收钱。

如何证一车一帅能够破双士将呢？